A Rolling Ball System. A conventional paradigm of linear oscillations is the motion of a small ball as it rolls on a parabolic curve with minimal energy dissipation. The unique minimum provides a compelling demonstration of stable equilibrium. If the curve is then shaken at close to the natural frequency of the ball then a large amplitude response occurs due to resonance may occur.

If we take this concept a couple of steps further we can envsion a small ball rolling along a two-dimensional surface, and furthermore, we can design the surface to exhibit various maxima and minima. Now, given some uncertainty in the initial conditions it can be very difficult to predict which long-term behavior (in this case a surface minimum) the ball will eventually end up in (given a little energy dissipation). And if we shake the surface harmonically (say) then chaos is a typical response.
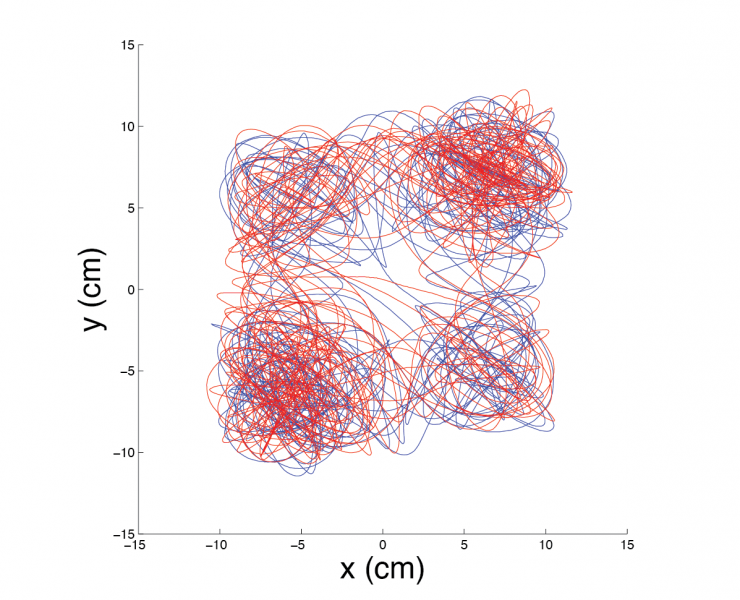
Here is a contour plot of the surface:
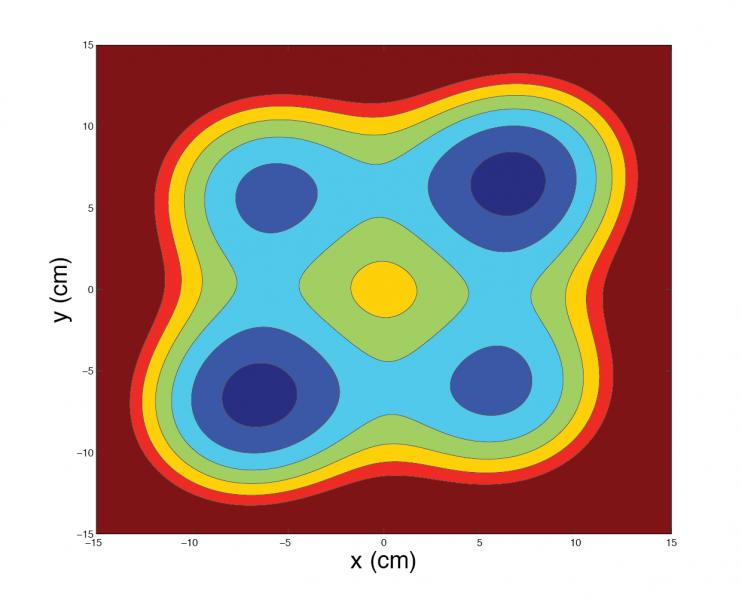
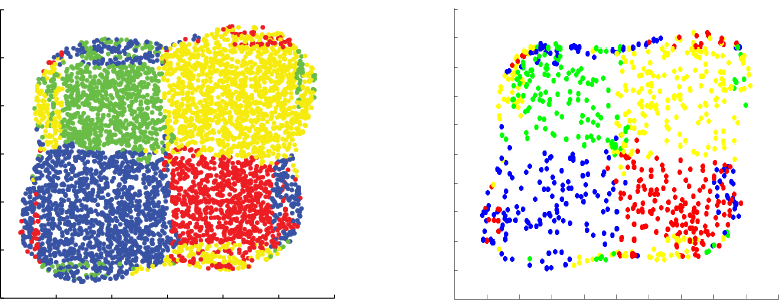
and the plots below show initial conditions for the unforced case in which the ball ends up in one of the four minima due to energy dissipation. In these cases the ball is started from rest, i.e., the initial velocity components are zero.
The forced case can produce chaos, first shown as time series and then as phase trajectories:
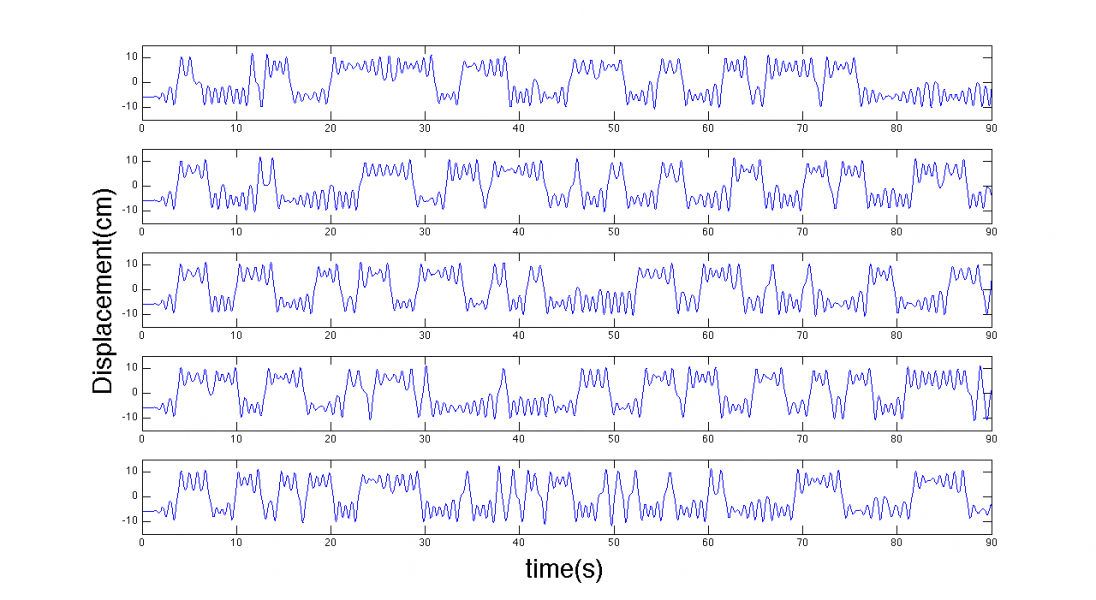
In the phase projection trajectories overlap (the phase space is 5-dimensional). In both cases (red and blue) the ball is at rest when the forcing is switched on (at the same forcing phase). The inevitable (tiny) difference leads to exponentially diverging behavior - a hallmark of chaos.